Question

Suppose f(x)=x^2 and g(x)=5x^2. which statement best compares the graph of g(x) with the graph of f(x)?

a) the graph of g(x) is the graph of f(x) horizontally stretched by a factor of 5
b) the graph of g(x) is the graph of f(x) vertically compressed by a factor of 5
c) the graph of g(x) is the graph of f(x) vertically stretched by a factor of 5
d) the graph of g(x) is the graph of f(x) shifted 5 units right

Answer 1

Option c - The graph of g(x) is the graph of f(x) vertically stretched by a factor of 5.

Explanation:

Given : Suppose
`f(x)=x^2` and
`g(x)=5x^2`

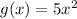
To find : Which statement best compares the graph of g(x) with the graph of f(x)?

Solution :

`f(x)=x^2` and
`g(x)=5x^2`

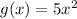
The graph of g(x) is multiplied by 5 of f(x) shows the vertical stretch.

Vertically stretch :

When y=f(x) → y=bf(x) i.e, the graph is b unit vertically stretched and b>1.

In the graph of
`f(x)=x^2` →
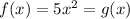`f(x)=5x^2=g(x)` i.e, 5 unit is multiplied.

Therefore, Option c is correct i.e, the graph of g(x) is the graph of f(x) vertically stretched by a factor of 5.

Answer 2

C

Explanation:

A vertical stretch of a function means the output values have changed by a factor or multiplication by a number. Recall, a quadratic function has the basic form
`f(x)=x^(2)`.

Our function g(x) is
`5x^(2)` meaning any value out of f(x) will be multiplied by 5 and the values increase by a factor of 5. This is a vertical stretch.

The statement that reads "the graph of g(x) is the graph of f(x) vertically stretched by a factor of 5" is correct.