Answer:
Value of x = 400
Explanation:
Joint variation states that describes a situation where a variable depends on two (or more) other variables, and varies directly with some of them.
Given: x varies directly with y and z.
i.e
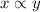 and
and

then we have the joint variation as;
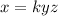 ......[1] where k is the constant variation.
......[1] where k is the constant variation.
Substitute the value of x =1200 when y =20 and z = 30 to solve for k;
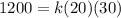
Simplify:
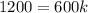
Divide both sides by 600 we get;

Now, substitute k =2 , y =10 and z = 20 to find x;
Using [1] we have;
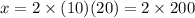
Therefore, the value of x is, 400