Question

A scientist is testing a new antibiotic by applying the antibiotic to a colony of 10,000 bacteria. The number of bacteria decreases by 75% every two hours. How many hours will it take for the bacteria colony to decrease to 1000? Round your answer to the nearest tenth of an hour.

Answer 1

3.3 hours.

Explanation:

We have been given that a scientist is testing a new antibiotic by applying the antibiotic to a colony of 10,000 bacteria. The number of bacteria decreases by 75% every two hours.

Since number of bacteria is decreasing exponentially, so we will use exponential decay function.

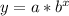`y=a*b^x`, where,

a= Initial value,

b = For decay b is in form (1-r), where r is rate in decimal form.

Let us convert our given rate in decimal form.

`75\%=(75)/(100)=0.75`

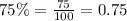
As number of bacteria is decreasing every 2 hours, so number of bacteria decreased in 1 hour will be x/2.

Upon substituting our given values in above formula we will get,

`y=10,000(1-0.75)^{(x)/(2)}`

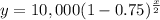
To find the number of hours it will take to for the bacteria colony to decrease to 1000, we will substitute y = 1,000 in our equation.

`1,000=10,000(0.25)^{(x)/(2)}`

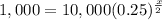
Let us divide both sides of our equation by 10,000.

`(1,000)/(10,000)=\frac{10,000(0.25)^{(x)/(2)}}{10,000}`

`0.1=(0.25)^{(x)/(2)}`

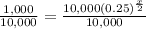
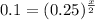
Let us take natural log of both sides of our equation.

`ln(0.1)=ln((0.25)^{(x)/(2)})`

`ln(0.1)=(x)/(2)*ln(0.25)`

`-2.302585=(x)/(2)*-1.386294`

`x=(-2.302585)/(-1.386294)*2`

`x=1.660964*2`

`x=3.3219\approx 3.3`

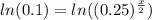
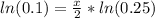
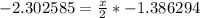
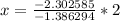
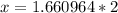
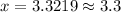
Therefore, it will take 3.3 hours for the bacteria colony to decrease to 1000.