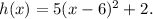Question

Given h(x)=5(x-6)^2+2 what transformations were done compared to the parent function f(x)=x^2?

Answer 1

1. Translation 6 units to the right.

2. Stretch by a factor 5.

3. Translation 2 units up.

Explanation:

Consider parent function
`f(x)=x^2.`

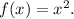
1. Translate the graph of the function 6 units to the right. Then you get the function
`f_1(x)=(x-6)^2.`

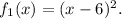
2. Stretch the graph of the function
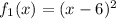`f_1(x)=(x-6)^2` by a factor 5 and get the function
`f_2(x)=5(x-6)^2.`

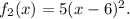
3. Translate the graph of the function
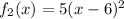`f_2(x)=5(x-6)^2` 2 units up to fet the function
`h(x)=5(x-6)^2+2.`