Question

asked Feb 10, 2019 158k views

1 Answer

Hitesh Prajapati · Answer 1 · 2019-02-16T13:02:47+0000

The smallest such number is 1055.

We want to find
such that

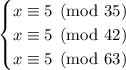
$\begin{cases}x\equiv5\pmod{35}\\x\equiv5\pmod{42}\\x\equiv5\pmod{63}\end{cases}$

The moduli are not coprime, so we expand the system as follows in preparation for using the Chinese remainder theorem.

$x\equiv5\pmod{35}\implies\begin{cases}x\equiv5\equiv0\pmod5\\x\equiv5\pmod7\end{cases}$

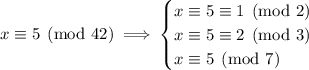
$x\equiv5\pmod{42}\implies\begin{cases}x\equiv5\equiv1\pmod2\\x\equiv5\equiv2\pmod3\\x\equiv5\pmod7\end{cases}$

$x\equiv5\pmod{63}\implies\begin{cases}x\equiv5\equiv2\pmod 3\\x\equiv5\pmod7\end{cases}$

Taking everything together, we end up with the system

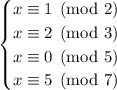
$\begin{cases}x\equiv1\pmod2\\x\equiv2\pmod3\\x\equiv0\pmod5\\x\equiv5\pmod7\end{cases}$

Now the moduli are coprime and we can apply the CRT.

We start with

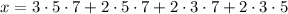
$x=3\cdot5\cdot7+2\cdot5\cdot7+2\cdot3\cdot7+2\cdot3\cdot5$

Then taken modulo 2, 3, 5, and 7, all but the first, second, third, or last (respectively) terms will vanish.

Taken modulo 2, we end up with

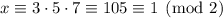
$x\equiv3\cdot5\cdot7\equiv105\equiv1\pmod2$

which means the first term is fine and doesn't require adjustment.

Taken modulo 3, we have

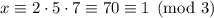
$x\equiv2\cdot5\cdot7\equiv70\equiv1\pmod3$

We want a remainder of 2, so we just need to multiply the second term by 2.

Taken modulo 5, we have

$x\equiv2\cdot3\cdot7\equiv42\equiv2\pmod5$

We want a remainder of 0, so we can just multiply this term by 0.

Taken modulo 7, we have

$x\equiv2\cdot3\cdot5\equiv30\equiv2\pmod7$

We want a remainder of 5, so we multiply by the inverse of 2 modulo 7, then by 5. Since
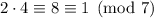$2\cdot4\equiv8\equiv1\pmod7$ , the inverse of 2 is 4.

So, we have to adjust
to

$x=3\cdot5\cdot7+2^2\cdot5\cdot7+0+2^3\cdot3\cdot5^2=845$

and from the CRT we find

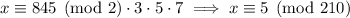
$x\equiv845\pmod2\cdot3\cdot5\cdot7\implies x\equiv5\pmod{210}$

so that the general solution
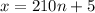x=210n+5 for all integers
.

We want a 4 digit solution, so we want

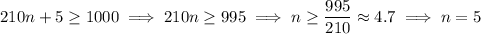
$210n+5\ge1000\implies210n\ge995\implies n\ge(995)/(210)\approx4.7\implies n=5$

which gives
$x=210\cdot5+5=1055$ .

Please log in or register to add a comment.