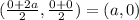Question

Given: The coordinates of triangle PQR are P(0, 0), Q(2a, 0), and R(2b, 2c). Prove: The line containing the midpoints of two sides of a triangle is parallel to the third side. As part of the proof, find the midpoint of PQ

Answer 1

To find the midpoint of PQ in the given triangle PQR, we use the midpoint formula, which states that the coordinates of the midpoint are the average of the x-coordinates and the average of the y-coordinates of the given points.

Step-by-step explanation:

To prove that the line containing the midpoints of two sides of a triangle is parallel to the third side, we need to show that the slope of the line is equal to the slope of the third side. Let's find the midpoint of PQ first.

The coordinates of P and Q are P(0, 0) and Q(2a, 0). The midpoint formula is given by:

Midpoint of PQ = ( (x1 + x2) / 2 , (y1 + y2) / 2 )

Substituting the values, we get Midpoint of PQ = ( (0 + 2a) / 2 , (0 + 0) / 2 ) = (a , 0)

Therefore, the midpoint of PQ is (a , 0).

Answer 2

Step-by-step explanation:

Given: In ΔPQR, the coordinates of the vertices are P(0, 0), Q(2a, 0), and R(2b, 2c).

To prove: The line containing the midpoints of two sides of a triangle is parallel to the third side.

Proof: In ΔPQR, the coordinates of the vertices are P(0, 0), Q(2a, 0), and R(2b, 2c).

Let, A, B and C be the mid-points of PQ, PR and QR respectively. Thus, the coordinates of S are:

`A=((0+2a)/(2),(0+0)/(2))=(a,0)`

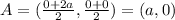
The coordinates of B are:

`B=((0+2b)/(2),(0+2c)/(2))=(b,c)`

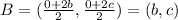
And the coordinates of C are:

`C=((2a+2b)/(2),(0+2c)/(2))=(a+b,c)`

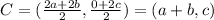
Now, slope of AB is given as:

`s={(c-0)/(b-a)}={(c)/(b-a)}`

And slope of QR is given as:

`s={(2c-0)/(2b-2a)}={(c)/(b-a)}`

Since the slopes of AB and QR are equal, hence they must be parallel.

Hence proved.

Also, Since A is the midpoint of PQ, therefore teh coordinates are:

A=
`((0+2a)/(2),(0+0)/(2))=(a,0)`