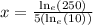Question

Using a logarithm, solve the following equation 500=(2)(10^5x) enter the value for x rounded to the nearest hundredth

Answer 1

0.48

Explanation:

The problem at hand

`500 = (2)(10^(5x))`

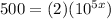
First divide out 2 on both side of the = sign

`500 = (2)(10^(5x))`

`(500)/(2) = ((2)(10^(5x)))/(2)`

`250 = 10^(5x)`

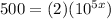
Now take the base 10 log on each side of the = sign

`\log_(10) (250) = \log_(10) (10^(5x))`

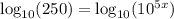
Now move the exponent to the left like so

`\log_(10) (250) = 5x \log_(10) (10)`

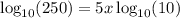
Rule you need to know.
`\log_a (a) = 1`

`\log_(10) (250) = 5x (\log_(10) (10))`

`\log_(10) (250) = 5x(1)`

`\log_(10) (250) = 5x`

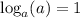
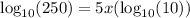
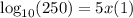
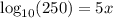
Now divide 5 from both sides of the equation

`(\log_(10) (250))/(5) = (5x)/(5)`

`(\log_(10) (250))/(5) = x`

`x = (\log_(10) (250))/(5)`

`x = 0.4795880017`

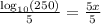
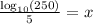
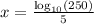
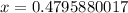
Round to nearest hundredths

`x = 0.48`

Side Note:

You could approach this problem in a different manner.

For instance, we could have done the following

`x = (\log_(10) (250))/(5(\log_(10) (10)))`

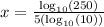
Also, you did not have to use log with a base 10. You could have used the natural log, which is
`\ln_e (x)`

`x = (\ln_(e) (250))/(5(\ln_(e) (10)))`