Answer:
The product of z1 and its conjugate is 25.
Explanation:
In the given graph x-axis represents the real axis and y-axis represents the imaginary axis.
The end point of z1 are (0,0) and (-4,-3). So, the complex number z1 is defined as
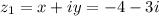
The conjugate of z1 is

The product of z1 and its conjugate is
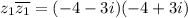
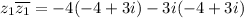
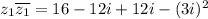
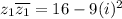
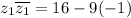
![[\because i^2=-1]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/muljom9yi415qk3cvrpuzv4hoymrrm413r.png)
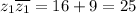
Therefore the product of z1 and its conjugate is 25.