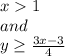Question

Can someone help me out with this? I’m not sure what I’m doing wrong.

Which graph best represents the solution to this system of inequalities?
2x + 3y (> with line underneath) 2
3x - 4y (< with like underneath) 3

Answer 1

Explanation:

This is a system of inequalities such that:

`\left \{ {{2x+3y\geq 2} \atop {3x-4y\leq 3}} \right.`

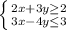
Let's start by solving for y for both equations:

Equation 1:

`2x+3y\geq  2\\\\3y\geq -2x+2\\\\y \geq (-2x+2)/(3)`

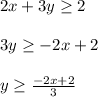
Equation 2:

`3x-4y\leq 3\\\\-4y\leq -3x+3\\\\y\geq -((-3x+3))/(4)`

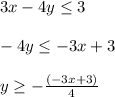
Now if we substitute the 2nd y into the first equation we obtain:

`2x+3((3x-3)/(4)) \geq  2\\\\2x+(9x-9)/(4)\geq 2\\\\(8x+9x-9)/(4)\geq 2\\\\17x-9\geq 8\\\\17x\geq 17\\\\x\geq 1`

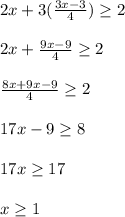
Now we will solve for the second equation using the first result of y and we obtain:

`3x-4((-2x+2)/(3)\leq 3\\\\3x+(8x-8)/(3)\leq 3\\\\(9x+8x-8)/(3)\leq 3\\\\17x-8\leq 9\\\\17x\leq 17\\\\x\leq 1`

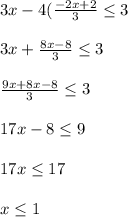
And so our solution for the system of equations is:

`x \leq 1\\and \\y\geq (-2x+2)/(3)`

As well as:

`x>1\\and\\y\geq (3x-3)/(4)`