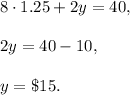Question

A local bake shop sells cookies and cakes.On monday , sean bought 3 cookies and 5 cakes and spent $78.75 on tuesday , sean bought 8 cookies and 2 cakes and spent $40 . Find the price of one cookie and one cake .

Answer 1

The price of one cookie is $1.25 and the price of one cake is $15.

Explanation:

Let $x be the price of one cookie and $y be the price of one cake.

1. On Monday, Sean bought 3 cookies and 5 cakes, then he spent $(3x+5y) and this is $78.75. Thus,

`3x+5y=78.75.`

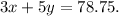
2. On Tuesday, Sean bought 8 cookies and 2 cakes, then he spent $(8x+2y) and this is $40. Thus,

`8x+2y=40.`

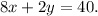
3. Solve the system of two equations:

`\left\{\begin{array}{l}3x+5y=78.75\\8x+2y=40\end{array}\right.`

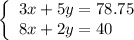
Multiply the first equation by 2 and the second equation by 5 and subtract them:

`2(3x+5y)-5(8x+2y)=2\cdot 78.75-5\cdot 40,\\ \\6x+10y-40x-10y=157.5-200,\\ \\-34x=-42.5,\\ \\x=\$1.25.`

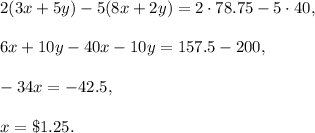
Then

`8\cdot 1.25+2y=40,\\ \\2y=40-10,\\ \\y=\$15.`