Answer:
The given sequence is geometric, which reason is -3.
Explanation:
If we pay attention to the sequence, we would observe that
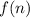 is increasing by a reason of
is increasing by a reason of
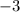 , because
, because

So, basically, each term is being multiplied by
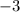 , that's what makes the sequence, which is a geometric sequence, because it's being built by a factor, that is, a number which multiplies each term.
, that's what makes the sequence, which is a geometric sequence, because it's being built by a factor, that is, a number which multiplies each term.
When you have to deduct if you have a arithmetic sequence or a geometric sequence, you need to observe if such sequence is increasing or decreasing faster. Like this case, you can see that the numbers are increasing rapidly, that means it's built based on a factor, not a difference, because when we use a difference to form a sequence, that will grow slower and it would be an arithmetic sequence.
Therefore, the given sequence is geometric, which reason is -3.