Question

What is the effect on the graph of the function f(x) = x when f(x) is replaced with -1/2 f(x)?

A) vertical reflection over x-axis and vertical stretch

B) vertical reflection over x-axis and vertical compression

C) horizontal reflection over y-axis and horizontal stretch

D) horizontal reflection over y-axis and horizontal compression

Answer 1

The correct option is B.

Explanation:

The given function is

`f(x)=x`

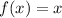
The new function is

`g(x)=-(1)/(2)f(x)`

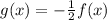
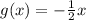`g(x)=-(1)/(2)x` .... (1)

It is in the form of

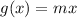`g(x)=mx` .... (2)

Where, m is a constant.

If m is negative, then there is a vertical reflection over x-axis. If the constant is greater than 1, we get a vertical stretch and if the constant is between 0 and 1, we get a vertical compression.

From (1) and (2), we get

`m=-(1)/(2)`

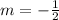
Since the value of m is negative and absolute value of m is between 0 and 1, therefore the graph g(x) shows the vertical reflection over x-axis and vertical compression.

Option B is correct.