Answer:
C) horizontal reflection over y-axis and horizontal stretch
Explanation:
1a- A vertical reflection over the x-axis occurs when a function
 is transformed into
is transformed into
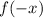
1b- A horizontal reflection over the y-axis occurs when a function
 is transformed into
is transformed into
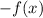
2a- A function is being compressed if
 is multiplied by a positive factor k:
is multiplied by a positive factor k:
 with
with
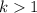
2b- A function is being stretched if
 is multiplied by a positive factor k:
is multiplied by a positive factor k:
 with
with
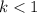
In our problem, the original function
 is:
is:
- Multiplied by 1/2, so by a factor which is smaller than 1, so we are in case 2b
- Transformed from
 into
into
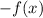 (due to the negative sign in front of it), so we are in case 1b
(due to the negative sign in front of it), so we are in case 1b
So, overall, we had a horizontal reflection over the y-axis and a stretch of the function.