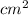Question

Point E is the midpoint of side BC of parallelogram ABCD (labeled counterclockwise) and AE ∩ BD =F. Find the area of ABCD if the area of △BEF is 3 cm2.

Answer 1

Answer:
`36 cm^2`

Step-by-step explanation:

Since here ABCD is the parallelogram.

Where E is the mid point of the line segment BC.

And, F is the intersection point of the segments AE and BD,

Also, Area of △BEF is 3
`cm^2`.

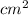We have to find Area of parallelogram ABCD.

Since,In ΔBEF and ΔACD,

∠ADF=∠EBF ( because AD ║ BE )

∠DFA = ∠BFE (vertically opposite angle)

Thus, By AA similarity postulate,

`\triangle BEF \sim \triangle ACD`,

Thus,
`(area of \triangle ADF )/(area of \triangle BFE) =((AD)/(BE))^2`

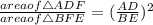
But, AD = 2 BE,

Therefore,
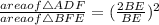`(area of \triangle ADF )/(area of \triangle BFE) =((2BE)/(BE))^2` = 4/1

Thus, area of Δ ADF =
`12 cm^2`

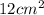
Similarly,
`\triangle ADB \sim \triangle BAE`

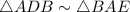
Now, let the area of the triangle AFB = x
`cm^2`

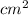
Thus, x + 12 = 2(x+3) ( because the area of the ΔADB = 2(area of ΔBAE) )

⇒ x = 6
`cm^2`

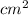
Therefore, area of ΔAFB= 6
`cm^2`

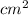
⇒ area of ΔABD = 12 + 6 = 18
`cm^2`

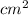
By the definition of diagonal of parallelogram,

Area of parallelogram ABCD = 2× area of Δ ABD= 2 × 18 = 36
`cm^2`