Answer: We can plot the graph with help of below explanation.
Explanation:
Since, given equation of polynomial,
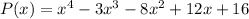
End behavior : Since, the leading coefficient of the polynomial is positive and even.
Therefore, the end behavior of the polynomial is,
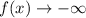 as
as
And,
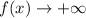 as
as
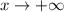
Points of the curve : since, P(4) = 0
Therefore, (x-4) is the multiple of P(x),
And we can write,
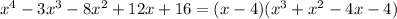
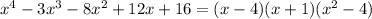
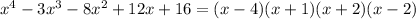
Thus, the roots of equation are 4, 2, -1 and -2.
Therefore, x-intercepts of the polynomial are (4,0) (2,0) (-1,0) and (-2,0)
Also, the y-intercept of the polynomial is ( 0,16)
Thus, we can plot the graph with help of the above information.