Answer:
a. -2, even mult. and 1, odd mult.
b.
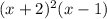
c. Odd degree of 3 or higher, likely higher due to the turns in the graph.
Explanation:
A polynomial graph has several features we look for to determine the equations.
- The zeros of the function are the x-intercepts. If the x-intercepts touch but do not cross then the intercepts have an even multiplicity like 2, 4, 6, etc. If the x-intercepts cross over then they have an odd multiplicity.
- Degree is the exponent or multiplicity of each zero. Therefore if we know the multiplicity of each zero we can add them together to find or make an educated guess for the degree of the entire polynomial.
- The shape of the graph tells us what type of polynomial. Odd degrees have a backwards S shape. Even degrees have a W shape. The shape can even tell us the if the equation has a positive or negative leading coefficient. Upside down W or an M shape is negative. While a sideways S shape is negative.
In this graph, there are two real zeros: -2,1
We can write them in intercept or factored form as (x-1) and (x+2).
Because the graph never crosses the x-axis at x=-2 the zero has an even multiplicity of at least 2. The opposite is true for x=1 because it crosses. Therefore it has an odd multiplicity of at least 1.
The graph is a sideways s shape and ends up so is positive.
This means the function has a degree of 3 or higher with the degree being odd.