Answer:
a. -1, odd; 2, even
b.
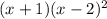
c. odd likely 3
Explanation:
A polynomial graph has several features we look for to determine the equations.
- The zeros of the function are the x-intercepts. If the x-intercepts touch but do not cross then the intercepts have an even multiplicity like 2, 4, 6, etc. If the x-intercepts cross over then they have an odd multiplicity.
- Degree is the exponent or multiplicity of each zero. Therefore if we know the multiplicity of each zero we can add them together to find or make an educated guess for the degree of the entire polynomial.
- The shape of the graph tells us what type of polynomial. Odd degrees have a backwards S shape. Even degrees have a W shape. The shape can even tell us the if the equation has a positive or negative leading coefficient. Upside down W or an M shape is negative. While a sideways S shape is negative.
In this graph, there are two real zeros: -1,2
We can write them in intercept or factored form as (x+1) and (x-2).
Because the graph crosses the x-axis at -1, it's multiplicity is odd likely 1. However, the graph does not cross at 2 and has an even multiplicity likely 2.
The graph is ends up and is a sideways s so is positive with an odd degree.
This means the function has a degree of 3 or higher with the degree being odd.