Question

What is the solution to the system of equations?

2x-3y+z=-19
5x+y-z=-7
-x+6y-z=35

A. (2,-6,-11)
B. (-2,6,3)
C. (6,2,-25)
D. (-2,6,9)

Answer 1

that answer is B because first u have to solve for Z in 2x-3y+Z=19

Z will be Z=-19-2x+3y

Answer 2

B. (-2,6,3)

Explanation:

First we will cancel the z-variable in the first two equations. We will do this by adding the second equation to the first:

`\left \{ {{2x-3y+z=-19} \atop {+(5x+y-z=-7)}} \right. \\\\7x-2y=-26`

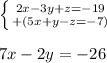
Next we cancel the z-variable in the bottom two equations. We will do this by subtracting the bottom equation from the middle one:

`\left \{ {{5x+y-z=-7} \atop {-(-x+6y-z=35)}} \right. \\\\6x-5y=-42`

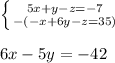
We can now take these equations without z as a system:

`\left \{ {{7x-2y=-26} \atop {6x-5y=-42}} \right.`

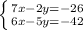
We will make the coefficients of y the same by multiplying the top equation by 5 and the bottom by 2:

`\left \{ {{5(7x-2y=-26)} \atop {2(6x-5y=-42)}} \right. \\\\\left \{ {{35x-10y=-130} \atop {12x-10y=-84}} \right.`

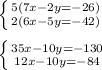
Next we subtract the bottom equation from the top:

`\left \{ {{35x-10y=-130} \atop {-(12x-10y=-84)}} \right. \\\\23x=-46`

Divide both sides by 23:

23x/23 = -46/23

x = -2

Substitute this into the first equation without z:

7(-2)-2y = -26

-14-2y = -26

Add 14 to each side:

-14-2y+14 = -26+14

-2y = -12

Divide both sides by -2:

-2y/-2 = -12/-2

y = 6

Substitute both x and y into our first original equation:

2(-2)-3(6)+z = -19

-4-18+z = -19

-22+z = -19

Add 22 to each side:

-22+z+22 = -19+22

z = 3