Answer:
Center (1,3) and radius 6
Explanation:
We must complete the square to find the center and radius of the circle.
First make sure the x and y squared terms have 1 as their coefficients. We also make sure x and y terms together.
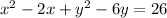
We now create space between the x and y terms with parenthesis.
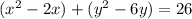
We complete the square by taking the middle terms -2x and the -6y - divide each and square them.
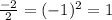
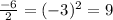
We add the squares to both sides.
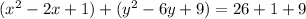
Simplify.
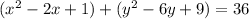
And write the quadratics in factored form.
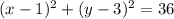
The center is (h,k) or (1,3). The radius is the square root of 36 which is 6.