Question

Which functions are continuous at x= -5? Select all that apply.

Answer 1

The correct ones i belive are B and C

Answer 2

option B and C

Explanation:

Lets check each function

Lets simplify
`(x^2-25)/(x+5)`

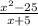
factor the numerator

`x^2-25 = (x+5)(x-5)`

`((x+5)(x-5)/(x+5)`

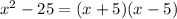
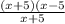
Cancel out x+5 so we are left with x-5

When x=-5 then f(x) = x-5= -5-5 = -10

To make the function continuous at x=-5 the value of f(x) should be -10

So option B is correct

Now we check with option C and D

Lets simplify
`(x^2+10x+25)/(x+5)`

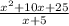
factor the numerator

`x^2+10x+25 = (x+5)(x+5)`

`((x+5)(x-5)/(x+5)`

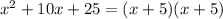
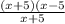
Cancel out x+5 , so we are left with x+5

When x=-5 then f(x) = x+5= -5+5 = 0

To make the function continuous at x=-5 the value of f(x) should be 0

So option C is correct