Question

Which equation has exactly two real and two non real solutions?

Answer 1

C. x^4 - 5x^2 - 36 = 0

Answer 2

`x^4-5x^2-36=0`

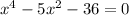
Explanation:

We need to find equation that has exactly two real and two non real solutions

2 real and 2 non real solution means 4 solutions

x^3 equation has maximum of 3 solutions

So we ignore equation that has largest exponent x^3

We ignore options B and D

Let check option A

`x^4 - 36x^2=0`

factor the left hand side

Factor out x^2

`x^2(x^2 - 36)=0`

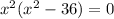
WE set each factor =0 and solve for x

x^2 =0 so x=0

x^2 - 36 =0 so x= +-6

So solutions are x=0, x=6 , x=-6. Only 3 real solutions we got

LEts check with option C

`x^4-5x^2-36=0`

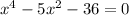
Factor left hand side

`(x^2-9)(x^2+4)=0`

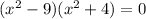
set each factor =0 and solve for x

x^2 -9 =0 so x= -3, + 3

x^2 + 4 =0 , x^2 = -4, so x= +2i, -2i

So we got two real solutions (-3,+3) and two non real solutions (-2i,+2i)