Answer:
0.034921 miles or 1843774 feet tall
Explanation:
Using trigonometric functions we know that
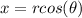 and
and
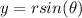 where
where
 =angle and r is the hypotenuse of the triangle.
=angle and r is the hypotenuse of the triangle.
First we will calculate the hypotenuse using the x equation, since we know x = 1 mile (distance from the building on the ground) we have:
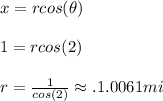
Now we will calculate the height of the building using the y equation and so:
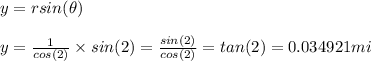
The building is 0.034921 miles or approximately 184.3774 feet tall.