Question

The value of a vintage car over time is represented by the function V(t)=24,300(1.37)t

, where t is the time in years.

What is the rate of increase?



Enter your answer in the box.

Answer 1

0.37 or 37%

Explanation:

I believe you meant to put
`V(t)=24300(1.37)^t`

The key thing here is look at the rate and we can do so by looking at the equation:

`A_(final)=A_(initial)(1+r)^t`

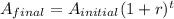
Where the initial amount the car was worth was $24,000. Now focus on the middle part of the equation (1 + r), 1 in this case means 100% of what the car is worth plus the interest rate. Simply put, to find out the rate we just need to subtract 1.37 - 1 = 0.37, meaning 37% (since 0.37 × 100 = 37%). This means that the car will increase in value by 37% every year, which is ridiculous!