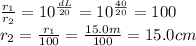Question

A laser produces light of wavelength lambda. The light is directed through two splits that are separated by a small distance. On the other side of the slits is an interference pattern of alternating dark(black) and bright bands. What is the wavelength of the light in the bright bands?

2lambda
Lambda
0.5 lambda
9 lambda
A train passes a farm house at 30.0 m/s and then the engineer sounds the 900-Hz whistle. The air is still and the speed of sound is 340 m/s. What frequency will a person inside the farmhouse hear? Assume that the angle between the farmhouse and the train is negligible.
883 Hz
827 Hz
877 hz(my choice)
871 Hz
You are 15.0 m from the source of a sound. At that distance, you hear it at a sound level of 20.0 dB. How close must you move to the sound to increase the sound level to 60 dB?
15.0 cm
45.0 cm
55.0 cm
60.0 cm
85.0 cm
Please help. I’ll really appreciate it.

Answer 1

1. Lambda

The phenomenon described in the problem is called diffraction.

Diffraction occurs when a wave 'bends' around an obstacle or a slit, producing an interference pattern beyond the obstacle/slit. In this example, a wave of light is made passing through two splits: each slit will act as a new source of the wave, producing waves with same wavelength (lambda), and the combination of the two waves produced by the two slits will generate interference on the sistance screen, producing the alternating black and bright bands. However, the diffraction effect does not change the wavelength of the original wave, so it is still lambda.

2. 827 Hz

This phenomenon is called Doppler effect: as the source of a sound moves relative to an observer, the apparent frequency heard by the observer is shifted with respect to the original frequency of the sound, according to the equation:

`f'=(v)/(v+v_s)f`

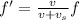
where

f is the original frequency of the wave

v is the speed of the wave

vs is the velocity of the source relative to the observer, and it is positive if the source is moving away from the observer and negative if it is moving towards the observer

In this problem, the speed of sound is v = 340 m/s. The original frequency of the train whistle is f = 900 Hz, and the velocity of the train relative to the farm house is
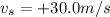`v_s = +30.0 m/s` (it is positive because the whistle is sounded after the train passes the house, so the train is moving away from the house). Substituting into the equation, we find:

`f'=(340 m/s)/(340 m/s + 30.0 m/s)(900 Hz)=827 Hz`

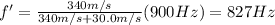
3. 15.0 cm

The difference in decibels between two sounds is given by:

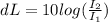`dL= 10 log ((I_2)/(I_1))` (1)

where I1 and I2 are the intensity of the two sounds.

The intensity of a sound is inversely proportional to the square of the distance from the source:

`I\propto (1)/(r^2)`

So the first equation can be rewritten as:

`dL= 10 log ((r_1^2)/(r_2^2)) = 10 log ((r_1)/(r_2))^2=20 log ((r_1)/(r_2))`

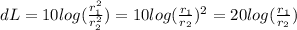
Here we know:

`dL=60 dB-20 dB=40 dB`

`r_1 = 15.0 m`

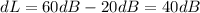
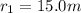
So we can re-arrange the previous equation to find the distance r2:

`(r_1)/(r_2)=10^{(dL)/(20)}=10^{(40)/(20)}=100\\r_2 = (r_1)/(100)=(15.0 m)/(100)=15.0 cm`