Answer:
Option C.
Explanation:
The standard form of a line is
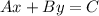
It a line passes through two points then the equation of line is
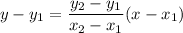
It is given that the line passes through the points (-3,1) and (3,2). So the equation of line is
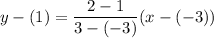

Multiply both sides by 6.
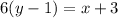
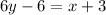
Subtract 6y and 3 from both sides.
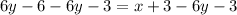

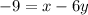
Interchange both sides.
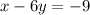
Therefore, the correct option is C.