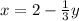Question

5-4. Solve each of the following equations for the indicated variable. Use your Equation Mat if it is helpful. Write down each of your steps algebraically. Solve for y: 2(y − 3) = 4 Solve for x: 2x + 5y = 10 Solve for y: 6x + 3y = 4y + 11 Solve for x: 3(2x + 4) = 2 + 6x + 10 Solve for x: y = −3x + 6

Answer 1

QUESTION 1

The given equation is :


`2(y - 3) = 4`
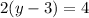
We want to solve for y. This means we have to isolate y on one side of the equation while all other constants are also on the other side of the equation,

We first divide both sides by 2 to obtain,


`(2(y - 3))/(2) = (4)/(2)`

We cancel out the common factors to get,


`y - 3 = 2`

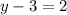
We now group like terms to get,


`y = 3 + 2`

We simplify to obtain,


`y = 5`

QUESTION 2

The given equation is


`2x + 5y = 10`
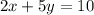
We want to solve for x. This means that we need to isolate x on one side of the equation, while all other variables and constant are also on the other side of the equation.

This implies that,


`2x= 10 - 5y`

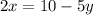
We now divide through by 2, to obtain,


`(2x)/(2) = (10)/(2) - (5y)/(2)`

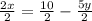
This will now give us,


`x = 5 - (5)/(2) y`

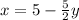
QUESTION 3

The given equation is

`6x + 3y = 4y + 11`

We want to solve for y. This means that we need to isolate y on one side of the equation, while all other variables and constants are also on the other side of the equation.

We first of all group all the y terms on one side of the equation to obtain,


`6x - 11 = 4y - 3y`

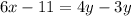
We simplify to get,


`6x - 11 = y`

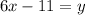
This implies that,


`y = 6x - 11`

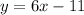
QUESTION 4

The given equation is,


`3(2x + 4) = 2 + 6x + 10`

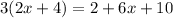
We want to solve for x. This means that we need to isolate x on one side of the equation, while all other variables and constant are also on the other side of the equation.

Let us first expand the brackets to get,


`6x + 12 = 2 + 6x + 10`
This implies that


`6x + 12 = 6x + 12`

We group like terms to get,


`6x - 6x = 12 - 12`

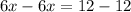
We now simplify both sides to get,


`0x = 0`

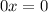
We don't want x to vanish, so let us try to divide both sides by zero to get,


`x = (0)/(0)`

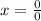
This is an indeterminate form, which implies that, x has infinitely many solutions. This means that all the real numbers are solution to the equation.


`\therefore \: x \in \: R`

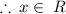
QUESTION 5

The given equation is,


`y = - 3x + 6`

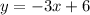
We want to solve for x, so we add the additive inverse of 6, which is -6 to both sides of the equation to get,


`y - 6 = - 3x`

We rewrite this to obtain,


`- 3x = y - 6`

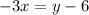
We divide through by -3 to get,


`( - 3x)/( - 3) = (y)/( - 3) - (6)/( - 3)`

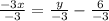
This will give us,


`x = - (y)/(3) + 2`

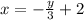
or


`x= 2 - (1)/(3) y`