Question

How much would Vincent have in his account after three years if he started with $100 and earns 5 percent, compounding annually?

$15.16
$105.00
$500.00
$115.76

Answer 1

15.16

Explanation:

quizlet.

Answer 2

D. $115.76

Explanation:

We will use compound interest formula to solve our given problem.

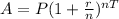`A=P(1+(r)/(n))^(nT)`, where,

A= The final amount after T years.

P= Principal amount.

r= Interest rate in decimal form.

n= Period of compounding.

T= Time in years.

Let us convert our given interest rate in decimal form.

`5\text{ percent}=(5)/(100)=0.05`

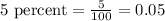
Now let us substitute our given values in compound interest formula.

`A=100*(1+(0.05)/(1))^(1*3)`

`A=100*(1+0.05)^(3)`

`A=100*(1.05)^(3)`

`A=100*1.157625`

`A=115.7625\approx 115.76`

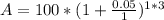
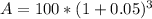
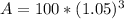
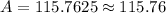
Therefore, Vincent will have $115.76 in his account after 3 years and option D is the correct choice.