Question

1. Solve the system using elimination

-4x + 4y = -8
x = 4y = -7

2. What is the solution of the system? Write answer in (x,y) form.

-8x + 2y = -26
-5x - 5y = -10

3. Solve the system using an equivalent system.

3x - 5y = 9
3x - y = -3

4. What are the solutions of the following systems?

-x + y = -2
4x - 4y = 8

Answer 1

1. (7.4,3.6)

2. (3,-1)

3. (-2,-3)

4. Infinite number of solutions.

Explanation:

We can solve systems of equations 3 ways: graphing, substitution, and elimination. We will solve 1-2, 4 using substitution and 3 with elimination.

1. Since x=4y-7, we substitute it in for x . It's better than elimination because of how it is set-up unless there is a typo.

• So -4x+4y=-8 becomes -4(4y-7)+4y=-8.
• We simplify to -14y+28+4y=-8.
• We add like terms to get -10y+28=-8.
• We now solve for y by subtracting 28 and dividing by -10.
• -10y+28-28=-8-28
• -10y=-36
• y=3.6
• We substitute y=3.6 into x=4y-7. x=4(3.6)-7=14.4-7=7.4

2. Since none of the coefficients of x & y are the same, we will rearrange and substitute.

• -8x+2y=-26 becomes 2y=8x-26 by adding 8x to both side.
• We divide by 2. y=4x-13.
• We substitute into -5x-5y=-10. -5x-5(4x-13)=-10
• We simplify to -5x-20x+65=-10
• We add like terms. -25x+65=-10
• We now solve for x by subtracting 65 and dividing by -25.
• -25x+65-65=-10-65
• -25x=-75
• x=3
• We substitute x=3 into -8(3)+2y=-26
• -24+2y=-26
• 2y=-2
• y=-1

3. We can solve this system through elimination. We subtract or add the equations when the coefficients are the same to eliminate one variable.

• 
  `-\left \{ {{3x-5y=9} \atop {3x-y=-3}} \right.`
• 
  `-4y=12\\y=-3`
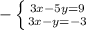
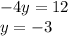
• We susbstitute y=-3 into one of the equations 3x-(-3)=-3.
• 3x=-6
• x=-2

4. Since none of the coefficients of x & y are the same, we will rearrange and substitute.

• -x+y=-2 becomes y=x-2
• We substitute into 4x-4(x-2)=8.
• Simplify 4x-4x+8=8.
• Add like terms 0x+8=8
• 8=8
• This is a true statement and a special solution. It means infinite number of solutions.