Question

Which rule yields the dilation of the figure STUV centered at the origin? A) (x, y) → (5x, 5y) B) (x, y) → (0.2x, 0.2y) C) (x, y) → (x + 5, y + 5) D) (x, y) → (x + 0.2, y + 0.2)

Answer 1

B. .2x, .2y

Explanation:

took test

Answer 2

Option B is correct.

Rule of dilation of the figure STUV is:
`(x, y) \rightarrow (0.2x , 0.2y)`

Explanation:

From the given figure;

the coordinates of STUV pre -image are;

S = (-5 , -5) ,

T = (5, -5)

U = (10 , 5)

V = (-10 , 5)

And the coordinates of dilated image S'T'U'V' are;

S' = (-1, -1)

T' = (1, -1)

U' = (2, 1)

V' = (-2, 1)

The rule of dilation with scale factor k centered at the origin is given by:

`(x, y) \rightarrow (kx , ky)`

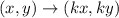
To solve for k;

Let any pre-image S(x, y)= (-5, -5)

here, x = -5 and y = -5

then;

S'(kx, ky) = (-1, -1)

Substitute value of x and y we get;

(-5k , -5k) = (-1, -1)

On comparing both sides we get;

-5 k = -1

Divide both sides by -5 we get;

`k= (-1)/(-5) = (1)/(5) = 0.2`

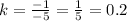
Therefore, the rule which yields the dilation of the figure STUV centered at the origin is;
`(x, y) \rightarrow (0.2x , 0.2y)`