Question

At a distance of 1 A.U., the earth takes one year to travel around the sun. How far away is a planet that takes eight years to go around the sun?

Answer 1

4

Step-by-step explanation:

Answer 2

4 AU

Step-by-step explanation:

We can solve the problem by using Kepler's third law, which states that the ratio between the square of the period of revolution of a planet around the Sun and the cube of its average distance from the Sun is constant for every planet orbiting the Sun:

`(T^2)/(r^3)=k`

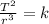
where

T is the orbital period

r is the average distance of the planet from the Sun

If we take two planets 1 and 2, the equation can be rewritten as

`(T_1^2)/(r_1^3)=(T_2^2)/(r_2^3)`

In this problem, we have:

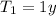`T_1 = 1 y` is the orbital period of the Earth

`r_1 = 1 AU` is the distance of the Earth from the Sun

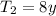`T_2 = 8 y` is the orbital period of the second planet

Therefore, we can re-arrange the equation to calculate r2, the averag distance of the other planet from the Sun:

`(r_2^3)/(T_2^2)=(r_1^3)/(T_1^2)\\r_2 = \sqrt[3]{(r_1 ^2 T_2^2)/(T_1^2)}=\sqrt[3]{((1 AU)^3(8 y)^2)/((1 y)^2)} =4 AU`