Question

A line passes through (3, -2) and (6, 2). a. Write an equation for the line in point-slope form. b. Rewrite the equation in standard form using integers

Answer 1

(a)

Given: A line passes through the points (3, -2) and (6, 2)

Point slope form: An equation of line passing through two points
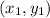`(x_1, y_1)` and
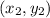`(x_2, y_2)` is given by:

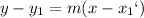`y -y_1=m(x-x_1`)` .....[1] where m is the slope of the line.

Calculate first the slope of the line:

Slope(m) =
`(y_2-y_1)/(x_2-x_1)`

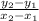
Substitute the given points;

`m = (2-(-2))/(6-3)=(2+2)/(3) =(4)/(3)`

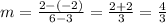
Substitute the value of m in [1] ;

`y - (-2) = (4)/(3)(x-3)`

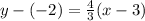
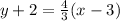`y+2=(4)/(3)(x-3)` ......[1]

therefore, the equation of line in point slope form is,
`y+2=(4)/(3)(x-3)`

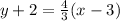
(b)

to find the standard form of the equation [1]

Multiply both sides by 3 in [1] we get;

`3(y+2) = 4(x-3)`

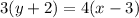
using distributive property;
`a\cdot (b+c) = a\cdot b + a\cdot c`

3y + 6 = 4x -12

Subtract 3y to both sides we get;

3y + 6 -3y = 4x - 12 - 3y

Simplify:

6 = 4x - 3y -12

Subtract 6 from both sides we get;

0 = 4x - 3y -12-6

Simplify:

4x - 3y - 18 =0

Therefore, the standard form of the equation is; 4x - 3y - 18 =0