Question

Which statement best describes why there is no real solution to the quadratic equation y = x^2 - 6x + 13?

The value of (-6)2 - 4 • 1 • 13 is a perfect square.
The value of (-6)2 - 4 • 1 • 13 is equal to zero.
The value of (-6)2 - 4 • 1 • 13 is negative.
The value of (-6)2 - 4 • 1 • 13 is positive.

Answer 1

The value of (-6)2 - 4 • 1 • 13 is negative.

Explanation:

To solve a quadratic equation we can solve by factoring, graphing or through the quadratic formula. The formula is as follows:

`x=\frac{-b+/-\sqrt{b^(2)-4ac } }{2a}`

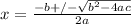
When the square root value is less than 0, a real solution cannot be found. This means when
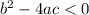`b^(2)-4ac<0`. For the equation, a=1, b=-6 and c=13.

We substitute and simplify.

`b^(2)-4ac=(-6)^2-4(1)(13)=36-4(13)=36-52=-16`

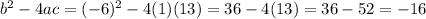
This gives us an imaginary solution because the value of (-6)2 - 4 • 1 • 13 is negative.