Question

Given: ABC is a right triangle with right angle C. AB=18 centimeters and m∠A=22∘ .

What is BC ?

Enter your answer, rounded to the nearest tenth, in the box.

Answer 1

Answer: 6.7cm

Step-by-step explanation: I took the K12 test.

Answer 2

BC = 6.7 cm (rounded to nearest tenth)

Step-by-step explanation:

Given: ABC is a right triangle with right angle C as shown below.

Side AB=18 cm and m∠A=22°.

Using Sine ratio in triangle ABC to find BC.

Sine ratio is defined as the ratio of the opposite side of a right triangle to the hypotenuse.

i.e

`\sin A = (Opposite side)/(Hypotenuse side)`

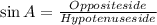
Let BC = x (opposite side) and AB = 18 cm(Hypotenuse side)

then;

`\sin 22^(\circ) = (x)/(18)`

`0.37460659341 = (x)/(18)`

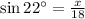
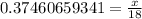
Multiply both sides by 18 we get;

`x = 0.37460659341 * 18 = 6.74291868`

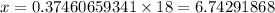
therefore, value of BC (nearest tenth place) is, 6.7 cm