Question

The top of a desk is shaped like a trapezoid. The bases of the trapezoid are 26.5 and 30 centimeters long. The area of the desk is 791 square centimeters long. The height of the trapezoid is the width of the desk. Write and solve an equation to find the width of the desk. Please find an answer that actually helps..Thanks

Answer 1

28 centimeters.

Step-by-step explanation:

Let w be width of desk.

We have been given that the bases of the trapezoid are 26.5 and 30 centimeters long. The area of the desk is 791 square centimeters long.

Since the area of trapezoid is half the sum of parallel sides times its height.

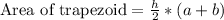`\text{Area of trapezoid}=(h)/(2)*(a+b)`, where

h= Height of trapezoid,

a and b= Length of parallel sides of trapezoid.

We have been given that the height of the trapezoid is the width of the desk.

Upon substituting our given vales in above formula we will get,

`791=(w)/(2)*(26.5+30)`

`791=(w)/(2)*(56.5)`

`791=w*28.25`

`w=(791)/(28.25)`

`w=28`

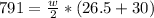
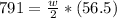
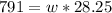
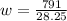
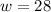
Therefore, the width of trapezoid is 28 centimeters.