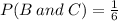Question

Consider a situation in which P(A) = 1/8, P(C) = 1/4, and P(A and B) = 1/12. What is P(B and C)?

Answer 1

1/6

Explanation:

Answer 2

ANSWER


`P(B \: and \: C) = (1)/(6)`


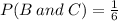
EXPLANATION

Recall that,


`P(A \: and \: B)=P(A) * P(B)`

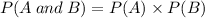
But we were given that,


`P(A)= (1)/(8)`

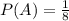
and


`P(A \: and \: B) = (1)/(12)`


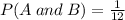
We substitute these values into the above formula to obtain,



`(1)/(12) = (1)/(8) * P(B)`



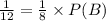
This implies that,


`(1)/(12) * 8=8 * (1)/(8) * P(B)`



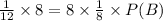
This simplifies to,


`P(B) = (8)/(12)`



`P(B) = (2)/(3)`


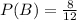
So we can now find

`P(B \: and \: C).`



We use the same formula again,


`P(B \: and \: C) = P(B) * P(C)`
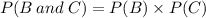
We substitute the values to get,



`P(B \: and \: C) = (2)/(3) * (1)/(4)`
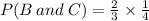
We multiply out to get,



`P(B \: and \: C) = (1)/(6)`