Question

Determine the heat given off to the surroundings when 9.873 g of aluminum reacts according to the equation 2Al + Fe2O3 → Al2O3 + 2Fe, ΔH°rxn= -849.1 kJ/mol.

Answer 1

Answer : The heat given off to the surroundings will be, -155.38 KJ

Solution : Given,

`\Delta H^o_(rxn)=-849.1KJ/mole`

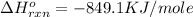
Mass of aluminium = 9.873 g

Molar mass of aluminium = 27 g/mole

First we have to calculate the moles of aluminium.

`\text{ Moles of Al}=\frac{\text{ Mass of Al}}{\text{ Molar mass of Al}}=(9.873g)/(27g/mole)=0.366moles`

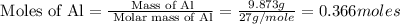
The given balanced reaction is,

`2Al+Fe_2O_3\rightarrow Al_2O_3+2Fe`

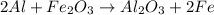
From the reaction, we conclude that

2 moles of aluminum releases heat energy = -849.1 KJ

0.366 moles of aluminium releases heat energy =
`(-849.1KJ)/(2moles)* 0.366moles=-155.38KJ`

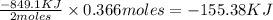
Therefore, the heat given off to the surroundings will be, -155.38 KJ