Question

Simplify the following expression. 4a^-2b

A.) b/4a^2
B.)4b/a^2
C.)1/4a^b2

Answer 1

B.)4b/a^2

Explanation:

Answer 2

ANSWER

The correct answer is B


`\frac{4b}{ {a}^(2) }`


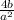
EXPLANATION

The given exponential expression is


`4 {a}^( - 2) b`

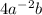
We can rewrite this as,


`4b * {a}^( - 2)`

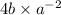
We need to simplify to obtain a positive index, so we apply the following property,



`{a}^( - m) = \frac{1}{ {a}^(m) }`

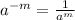
This implies that,



`4b * {a}^( - 2) = 4b * \frac{1}{ {a}^(2) }`

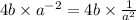
This will finally simplify to,


`4b * {a}^( - 2) =\frac{4b}{ {a}^(2) }`


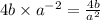
Therefore the correct answer is B