Question

In a trapezoid the lengths of bases are 11 and 18. The lengths of legs are 3 and 7. The extensions of the legs meet at some point. Find the length of segments between this point and the vertices of the greater base.

Answer 1

The length of segments between this point and the vertices of the greater base are 7.714 and 17.

Explanation:

Draw a figure and mark each vertex.

Let length of AP be x and length of BP be y.

in triangle APB and DPC.

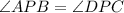`\angle APB=\angle DPC` (Common angle)

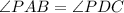`\angle PAB=\angle PDC` (Corresponding angle)

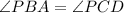`\angle PBA=\angle PCD` (Corresponding angle)

By, AA postulate triangle APB and DPC are similar triangle.

Since AB and and CD are parallel sides, therefore triangle ABP and DPC are similar triangle. So, their corresponding sides are proportional.

`(AP)/(PD)=(AB)/(DC)=(BP)/(PC)`

`(AP)/(PD)=(AB)/(DC)`

`(x)/(x+3)=(11)/(18)`

`18x=11x+33`

`7x=33`

`x=4.714`

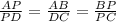
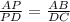
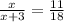
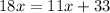
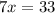
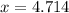
We have to find the length of DP.

`DP=AP+AD=4.714+3=7.714`

`(AB)/(DC)=(BP)/(PC)`

`(11)/(18)=(y)/(y+7)`

`11y+77=18y`

`77=7y`

`y=11`

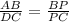
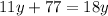
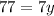
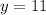
We have to find the length of CP.

`CP=PB+BC=11+7=17`

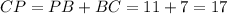
Therefore the length of segments between this point and the vertices of the greater base are 7.714 and 17.