Answer:
154 square inches
Explanation:
Watch the attached figure of the square pizza box and the largest pizza that can fit into it.
Let the each side of the square pizza box be a inches.
Radius of the largest pizza that can fit into it = Half of the side of the pizza box =
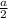
So, area of the square box = Side * Side
= a * a
= a² square inches
It has also been given that the large box has an area of 196 square inches.
So,
Area of the box = a²
=> 196 = a²
Flipping the sides of the equation, we get
=> a² = 196
Taking square root on both the sides,
√a² = √196
a = 14 inches
So,
Side of square box = 14 inches
Radius of the largest pizza that can fit into it =
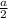
=
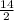
= 7 inches
Area of the largest possible pizza that could be placed into the box
= π *radius² [since pizza is circular in shape]
=
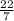 * 7²
* 7²
=
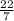 * 7 * 7
* 7 * 7
Cancelling out a pair of 7's from the top and bottom, we have
= 22 * 7
= 154 square inches