Answer:
The correct option is A. The median-median line regression line is a better prediction.
Explanation:
The given median-median line for a dataset is
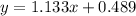
The least-squares regression line for the same dataset is
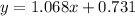
The given point is (50,60).
Substitute x=50 in each given equation.
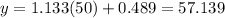
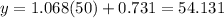
Since the value of median-median line at x=50 is near to 60 than the value of least-squares regression at x=50.
The median-median line regression line is a better prediction. Therefore the correct option is A.