Answer:
Perimeter of ΔAKL is,
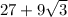 units.
units.
Area of ΔAKL is,
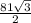 square units
square units
Explanation:
Given: In ΔAKL , AK = 9 units ,
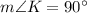 and
and
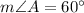 .
.
In ΔAKL
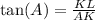
Substitute the value AK = 9 units and
 to solve for KL ;
to solve for KL ;

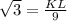
⇒

In right angle ΔAKL,
Using Pythagoras theorem;
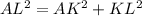 ......[1]
......[1]
Substitute AK = 9 units and
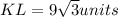 in [1] to solve for AL;
in [1] to solve for AL;

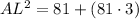

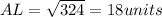
Perimeter of triangle is the sum of all the sides.
Perimeter of triangle AKL = AK +KL +AL =
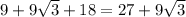 units.
units.
Formula for Area of right angle triangle is given by:
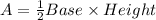
Area of triangle AKL=
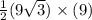
=
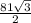 square units
square units