Question

In parallelogram ABCD , diagonals AC¯¯¯¯¯ and BD¯¯¯¯¯ intersect at point E, AE=x2−16 , and CE=6x . What is AC ? Enter your answer in the box.

Answer 1

96

Explanation:

Answer 2

AC = 96 units.

Explanation:

Given ABCD is a parallelogram.

And diagonals AC and BD intersects at point E.

Note: Diagonals of a parallelogram intersects at mid-point.

E is the mid point of diagonal AC

Therefore,

AE = CE.

Plugging expression for AE and CE, we get

`x^2-16 =6x.`

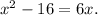
Subtracting 6x from both sides, we get

`x^2-16-6x = 6x-6x`

`x^2 -6x -16 =0`

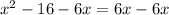
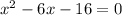
Factoring quadratic

(x+2)(x-8) =0.

x+2 =0 => x=-2.

x-8=0 => x=8.

We can't take the length by a negative number. Therefore, x=8.

Now, plugging x= 8 in CE =6x, we get

CE = 6(8) = 48.

We need to find the length of AC.

AC would be two times of CE.

Therefore, AC = 2 × 48 = 96.