Question

What is the centripetal force that would be required to keep a 4.0 kg mass moving in a horizontal circle with a radius of 0.80 meters at a speed of 6.0 meters/second?

A. 3.9 × 101 newtons tangent to the circle B. -3.0 × 101 newtons tangent to the circle C. 1.4 × 102 newtons radially outward D. 1.8 × 102 newtons radially inward E. 1.8 × 102 newtons radially outward

Answer 1

other guy is right

Step-by-step explanation:

Answer 2

D. 1.8 × 102 newtons radially inward

Step-by-step explanation:

The magnitude of the centripetal force is given by:

`F=m(v^2)/(r)`

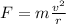
where

m is the mass of the object

v is the tangential speed

r is the radius of the circular trajector

In this problem, we have m = 4.0 kg, v = 6.0 m/s and r = 0.80 m, therefore substituting into the equation we get

`F=(4.0 kg)((6.0 m/s)^2)/(0.80 m)=180 N`

The centripetal force is the force that keeps the object in a circular trajectory, so it is a force that is always directed inward (towards the centre of the circular path) and radially. Therefore, the correct answer is

D. 1.8 × 102 newtons radially inward