Question

Two water jets are emerging from a vessel at a height of 50 centimeters and 100 centimeters. If their horizontal velocities at the point of ejection are 1 meter/second and 0.5 meters/second respectively, calculate the ratio of their horizontal distances of impact.

A. 1:04 B. 1:234 C. 2:01 D. 1.41:1 E. 3:02

Answer 1

Answer: The correct answer is option (D).

Step-by-step explanation:

Vertical distance of first water jet =
`y_1=50 cm`

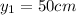
Vertical distance of second water jet =
`y_2=100 cm`

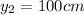
Horizontal velocity of first water jet =
`u_y_ 1=1 m/s`

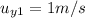
Horizontal velocity of second water jet =
`u_y_2=0.5 m/s`

Vertical distance of first water jet:

`y_1=(u_y_1)t_1+(1)/(2)gt_1^2`

`u_y_1=0,(u_y_1)t_1=0`

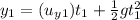
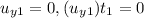
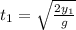`t_1=\sqrt{(2y_1)/(g)}`...(1)

Similarly, Vertical distance of second water jet:

`y_2=(u_y_2)t_2+(1)/(2)gt_2^2`

`u_y_2=0,(u_y_2)t_2=0`

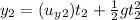
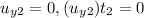
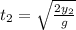`t_2=\sqrt{(2y_2)/(g)}`...(2)

Horizontal distance of first water jet:

`x_1=(u_x_1)t_1+(1)/(2)at_1^2`

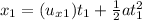
There is no acceleration in horizontal direction.

`a=0,at_1^2=0`

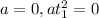
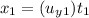`x_1=(u_y_1)t_1`...(3)

Horizontal distance of second water jet:

`x_2=(u_x_2)t_2+(1)/(2)at_2^2`

`a=0,at_2^2=0`

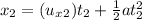
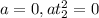
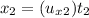`x_2=(u_x_2)t_2`...(4)

On dividing (3) and (4):

`(x_1)/(x_2)=((u_y_1)t_1)/((u_y_2)t_2)`

`(x_1)/(x_2)=(u_y_1)/(u_y_2)*\frac{\sqrt{(2y_1)/(g)}}{\sqrt{(2y_2)/(g)}}}=(u_y_1)/(u_y_2)\sqrt{(y_1)/(y_2)}`

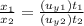
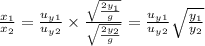
(from (1) and (2))

`(x_1)/(x_2)=(1 m/s)/(0.5 m/s)\sqrt{(50 cm)/(100 cm)}=1.41:1`

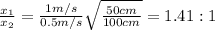
Hence, the correct answer is option (D).