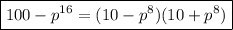Question

Which shows the factored form of the expression below? 100-p^16 (show all steps you took to get to answer)

Answer 1

`100-p^(16)=(10-p^(8))(10+p^(8))`

Explanation:

Factoring

Binomial factoring is a common task when solving a great variety of math problems.

One of the best-known formula that helps us to factor a binomial is:

`(a^2-b^2)=(a-b)(a+b)`

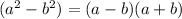
It can easily be identified because the expression is the difference between two perfect squares.

The expression

`100-p^(16)`

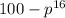
can be factored with the formula above since it's the difference of two squares:

`a=√(100)=10`

`b=\sqrt{p^(16)}=p^(8)`

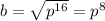
The expression is factored as follows:

`\boxed{100-p^(16)=(10-p^(8))(10+p^(8))}`