Answer:
The area of the smaller triangle is
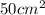
Explanation:
The given length of the bigger triangle is
 .
.
The length of the smaller triangle that corresponds to this side is
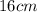 .
.
We can see that the scale factor for this enlargement (reduction) is
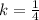 .
.
The scale factor for the area is
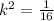 .
.
Therefore to obtain the area of the smaller triangle, we need to multiply the area of the bigger triangle by
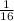 .
.
This implies that,
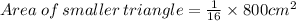

The correct answer is B