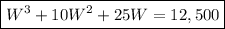Question

A shipping container in the shape of a rectangular prism must have a volume of 25,000 cubic feet. The client tells the manufacturer that, because of the contents, the length of the container must be 10 feet longer than twice the width w, and the height must be 5 feet greater than the width.

Find the equation, in terms of w, that could be used to find the dimensions of the container in feet. Your answer should be in the form of a polynomial equals a constant.

Answer 1

`W^3+10W^2+25W=12,500`

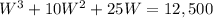
Explanation:

The Volume of a Rectangular Prism

Given a rectangular prism of width W, length L, and height H, the volume is computed with the formula:

`V=WLH`

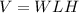
The shipping container must have the following conditions:

The length must be 10 ft longer than twice the width:

L = 2W + 10

The height must be 5 feet greater than the width:

H = W + 5

Substituting in the formula of the volume:

`V=W(2W+10)(W+5)`

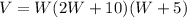
Multiplying:

`V=W(2W^2+10W+10W+50)`

`V=2W^3+10W^2+10W^2+50W`

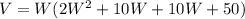
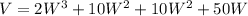
Simplifying:

`V=2W^3+20W^2+50W`

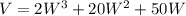
This volume is known to have a value of 25,000 cubic feet, thus:

`2W^3+20W^2+50W=25,000`

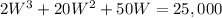
Dividing by 2:

`\boxed{W^3+10W^2+25W=12,500}`