Answer:
The missing terms of the geometric series are
A.

and
B.
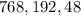
Explanation:
The given geometric sequence is
 .
.
The second and sixth term of the geometric sequence are
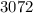 and
and
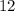 respectively.
respectively.
Recall that the nth term of a geometric sequence is given by,
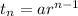 .
.
This implies that the second term will be,
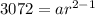 .
.
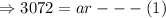 .
.
Also the 6th term is
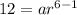 .
.
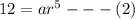 .
.
We divide equation (2) by (1) to get,
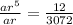

![\Rightarrow r=\pm \sqrt[4]{(1)/(256) }](https://img.qammunity.org/2019/formulas/mathematics/middle-school/683b38187ncdpr9o0mabjjf2opk9hg9les.png)
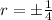
If
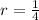
We get,
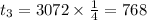
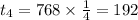

But If
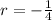
We get,
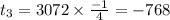
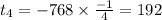

Therefore the correct answer is A and B.