To simplify
![\sqrt[4]{(24x^6y)/(128x^4y^5)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/1li3eyevqo2zz44f5956cfjy7ppr7srb6v.png)
we need to use the fact that
![\sqrt[4]{x^4}=|x|](https://img.qammunity.org/2019/formulas/mathematics/high-school/gjxea1gt68afyn9cg9d09rtx2ax4g9z6vb.png)
Why the absolute value? It's because
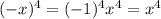 .
.
We start by rewriting as
![\sqrt[4]{(2^23x^6y)/(2^6x^4y^5)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/njqjtap1hm92hhukawkj2pynp2to99oaxf.png)
![\sqrt[4]{(2^23x^4x^2y)/(2^42^2x^4y^4y)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/ffwmyo6ai5dh1jpc2cbfa55ywxz21orwr5.png)
Since
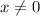 , we have
, we have
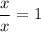 , and the above reduces to
, and the above reduces to
![\sqrt[4]{(3x^2y)/(2^4y^4y)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/yxoldxtjgsfpaot8jlb2udsbbn5ab6p7dp.png)
Then we pull out any 4th powers under the radical, and simplify everything we can:
![\frac1{\sqrt[4]{2^4y^4}}\sqrt[4]{(3x^2y)/(y)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/thfgvynt1s4yxyodnpjgeu7v52v497ydn4.png)
![\frac1\sqrt[4]{3x^2}](https://img.qammunity.org/2019/formulas/mathematics/high-school/o02ow9wyby7rrm6n5us8mldkardncj7upr.png)
where
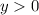 allows us to write
allows us to write
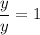 , and this also means that
, and this also means that
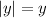 . So we end up with
. So we end up with
![\frac{\sqrt[4]{3x^2}}{2y}](https://img.qammunity.org/2019/formulas/mathematics/high-school/b7fjs3or88c1023ejj2mk935udbde9a8o2.png)
making the last option the correct answer.