ANSWER
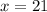
EXPLANATION
The two given angles are
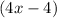
and
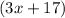
These two angles are vertically opposite to each other.
Recall that vertically opposite angles are equal.
We therefore write the equation below and use it to find x.
This implies that,
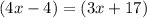
We group like terms to get,
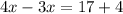
This implies that
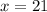
Therefore the correct answer is D.